Finding Roots of Quadratic Equation in C | C Program

Here's a C program to find the roots of a quadratic equation with output and proper explanation. This program uses Switch Case Condition, Break, IF-Else and Math.H Header File to use functions like pow() and sqrt().

General format of second degree quadratic equation -

Fig 1: Second Degree Quadratic Equation.

Roots of quadratic equation are - 

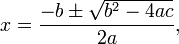Fig 2: Roots of  Quadratic Equation.

And discriminant can be calculated as - 

Fig 3: Discriminant of  Quadratic Equation.

# include <stdio.h>
# include <conio.h>
# include  
void main() 
{ 
 float a, b, c, d, real, imag, r1, r2, n ; 
 int k ; 
 clrscr() ; 
 printf("Enter the values of A, B & C : ") ; 
 scanf("%f %f %f", &a, &b, &c) ; 
 if(a != 0) 
 { 
  d = b * b - 4 * a * c ; 
  if(d < 0) 
   k = 1 ; 
  if(d == 0) 
   k = 2 ; 
  if(d > 0) 
   k = 3; 
  switch(k) 
  { 
   case 1 : 
     printf("\nRoots are imaginary\n") ; 
     real = - b / (2 * a) ; 
     d = - d ; 
     n = pow((double) d, (double) 0.5) ; 
     imag = n / (2 * a) ; 
     printf("\nr1 = %7.2f + j%7.2f", real, imag) ; 
     printf("\nr2 = %7.2f - j%7.2f", real, imag) ; 
     break ; 
   case 2 : 
     printf("\nRoots are real and equal\n") ; 
     r1 = - b / (2 * a) ; 
     printf("\nr1 = r2 = %7.2f", r1) ; 
     break ; 
   case 3 : 
     printf("\nRoots are real and unequal\n") ; 
     r1 = (- b + sqrt((double) d)) / (2 * a) ; 
     r2 = (- b - sqrt((double) d)) / (2 * a) ; 
     printf("\nr1 = %7.2f",r1) ; 
     printf("\nr2 = %7.2f",r2) ; 
     break ; 
  } 
 } 
 else 
  printf("\nEquation is linear") ; 
 getch() ; 
}

Output of above program is

 
Enter the values of A, B & C : 1.0     2.0      7.0
Roots are imaginary

r1 =   -1.00 + j   2.45
r2 =   -1.00 - j   2.45


Enter the values of A, B & C : 1.0      2.0      1.0
Roots are real and equal

r1 = r2 =   -1.00

Explanation of above program

Variables used in this program -

• a, b, c - are the coefficients of quadratic equation (see fig 1).
• d - is the discriminant of quadratic equation (see fig 3).
• real and imag - are the variables used only in the case when the roots of quadratic equation are imaginary. In that case real will contain the real part of the root and imag will contain the imaginary part of the root.
• r1 and r2 - are the two roots in case the roots of the equation are real.
• k - is used to switch between different cases based on the value of discriminant.

First we ask the user to enter the value of A, B and C coefficients. Next we check whether the value of variable a is zero or not using IF-Else condition. If the value of a is zero that means our equation is linear in nature i.e. bx + c and hence we print it out in the else part and terminate the program. Otherwise in the if part, we calculate the roots of the equation.

Inside IF, we first calculate the discriminant and store it in variable d. After calculating value of d we can decide which case to execute in the switch case condition - 

• If d < 0 i.e. roots are imaginary. So Case 1 is executed.
• If d = 0 i.e. roots are real and equal. So Case 2 is executed.
• If d > 0 i.e. roots are real and unequal. So Case 3 is executed.

Once the value of d is calculated the right case according to the value of d is executed and the roots are calculated according to the formula (see fig 2).

Note: If you notice in the line n = pow((double) d, (double) 0.5), you must be wondering what is the purpose of writing (double) d and (double) 0.5 instead of just d and 0.5. The reason is that we're casting the value of that variable. When we first declared the variable d it was of the type float. But now we want to use its value as a double so we're casting the value of variable d from type float to double. The same case is with the value 0.5.